Python数据结构__树

发布时间：2019-08-27 07:59:30编辑：auto阅读（1723）

树是一种非常重要的数据结构，它是非线性结构，它不是Python内置的数据结构；





树：

  1.非线性结构，每个元素可以有多个前驱和后继；

  2.树是n(n>=0)个元素的集合

    n=0时，称为空树；

    树只有一个特殊的没有前驱的元素，称为树的根Root；

    树中除了根结点外，其余元素只能有一个前驱，可以有零个或多个后继；

  3.递归定义

    树T是n(n>=0)个元素的集合。n=0时，称为空树。

    有且只有一个特殊元素根，剩余元素都可以划分为m个不相交的集合T1、T2、T3...Tm，

而每一个集合都是树，称为T的子树Subtree.

    子树也有自己的根。

---

---

树的概念






---

---

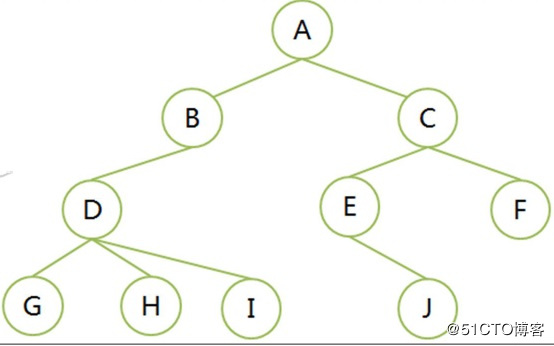
结点： 树中的数据元素


结点的度degree： 结点拥有的子树的数目称为度，记作d(v)

叶子结点： 结点的度为0，称为叶子结点leaf、终端结点、末端结点

分支结点： 结点的度不为0，称为非终端结点或分支结点

分支： 结点之间的关系

内部结点： 除根结点外的分支结点，当然也不包括叶子结点

树的度是树内各结点的度的最大值。D结点最大为3.树的度数就是3.

---

---

孩子(儿子Child)结点： 结点的子树的根结点成为该结点的孩子


双亲(父Parent)结点： 一个结点是它各子树的根结点的双亲

兄弟(Sibling)结点： 具有相同双亲结点的结点

祖先结点： 从根结点到该结点所经分支上所有的结点。A、B、D都是G的祖先的结点

子孙结点： 结点的所有子树上的结点都称为该结点的子孙。B的子孙是D、G、H、I

结点的层次(Level)： 根结点为第一层，根的孩子为第二层，以此类推，记作L(v)

树的深度(高度Depth): 树的层次的最大值。上图的树深度为4

堂兄弟： 双亲在同一层的结点

---

---

有序树： 结点的子树是有顺序的(兄弟有大小，有先后次序)，不能交换


无序树： 结点的子树是有无序的，可以交换

路径： 树中的k个结点n1、n2、...、nk，满足ni是n(i+1)的双亲，成为n1到nk的一条路径。就是一条线串下来的，


前一个都是后一个的父(前驱）结点。

路径长度 = 路径上结点数-1，也是分支数

森林：m(m>=0)棵不相交的树的集合

  对于结点而言，其子树的集合就是森林。A结点的2棵子树的集合就是森林。

---

---

树的特点：


  唯一的根

  子树不相交

  除了根以外，每个元素只能有一个前驱，可以有零个或多个后继

  根结点没有双亲结点（前驱），叶子结点没有孩子结点（后继）

  vi是vj的双亲，则L(vi) = L(vj)-1，也就是说双亲比孩子结点的层次上1

---

---

二叉树


  每个结点最多2棵子树

    二叉树不存在度数大于2的结点

  它是有序树，左子树、右子树是顺序的，不能交换次序

  即使某个结点只有一棵子树，也要确定它是左子树还是右子树




二叉树的五种基本形态

  空二叉树

  只有一个根结点

  根结点只有左子树

  根结点只有右子树

  根结点有左子树和右子树

---

---



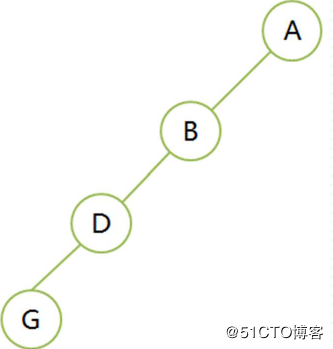
斜树：

  左斜树，所有结点都只有左子树；

  右斜树，所有结点都只有右子树；

---

---

满二叉树：

一棵二叉树的所有分支结点都存在左子树和右子树，并且所有叶子结点只存在在最下面一层。


同样深度二叉树中，满二叉树结点最多。

k为深度(1<=k<=n),则结点总数为2^k-1

如下图，一个深度为4的15个结点的满二叉树




---

---

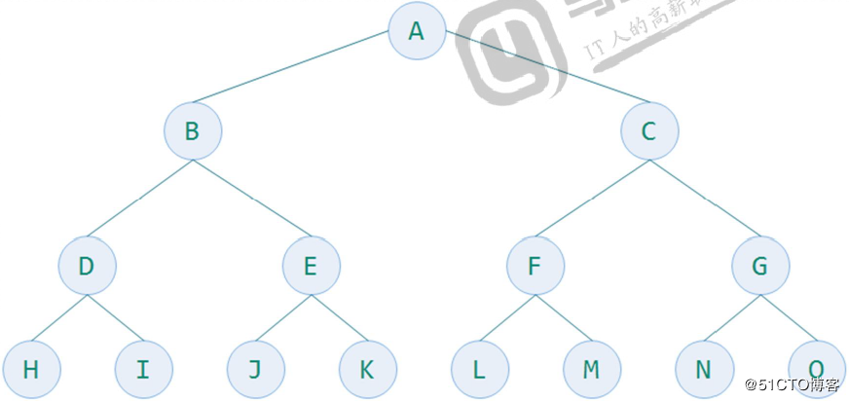
完全二叉树Complete Binary Tree

  若二叉树的深度为k，二叉树的层数从1到k-1层的结点数都达到了最大个数，在第k层的所有结点都集中在最左边，

这就是完全二叉树；

  完全二叉树由满二叉树引出；

  满二叉树一定是完全二叉树，但完全二叉树不是满二叉树；

  k为深度(1<=k<=n)，则结点总数最大值为2^k-1，当达到最大值的时候就是满二叉树；

---

二叉树的性质

  性质1：

  在二叉树的第i层上至多有2^(i-1)个结点(i>=1)

  性质2：

    深度为k的二叉树，至多有2^k-1个结点(k>=1)

  性质3：

    对于任何一棵二叉树T，如果其终端结点数为n0，度数为2的结点为n2，则有n0=n2+1

    换句话说，就是叶子结点数-1就等于度数为2的结点数；

    证明：

      总结点数为n=n0+n1+n2，n1为度数为1的总结点总数。

      一棵树的分支数为n-1，因为除了根结点外，其余结点都有一个分支，即n0+n1+n2-1

      分支数还等于n0*0+n1*1+n2*2,n2是2分支结点所以乘以2，2*n2+n1

      可得2*n2 + n1 = n0+n1+n2-1 => n2 = n0-1

  其它性质：

    高度为k的二叉树，至少有k个结点

    含有n(n>=1)的结点的二叉树高度至多为n。和一句一个意思

    含有n(n>=1)的结点的二叉树的高度至多为n，最小为math.ceil(log2（n+1))，不小于对数值的最小整数，向上取整。

---

---

完全二叉树性质


  性质1：

    具有n个结点的完全二叉树的深度为int(log2n)+1或者math.ceil(log2(n+1))

  性质2：

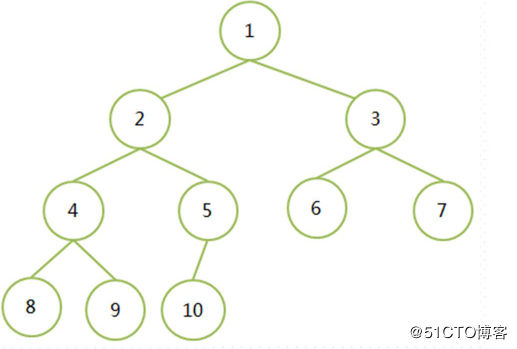
    如果有一棵n个结点的完全二叉树(深度为性质1)，结点按照层序编号，如下图

    如果i=1,则结点i是二叉树的根，无双亲；如果i>1，则其双亲是int(i/2)，向下取整。

    就是子节点的编号整除2得到的就是父结点的编号。父结点如是要是i，那么左孩子结点

    就是2i，右孩子结点就是2i+1

    如果2i>n，则结点i无左孩子，即结点i为叶子结点；否则其左孩子结点存在编号为2i

    如果2i+1>n，则结点i无右孩子，注意这里并不能说明结点i没有左孩子；否则右孩子结点存在

    编号为2i+1。



    

  

关键字：